T
Teach Me AnythingTMA
Video History
Page 1 / 44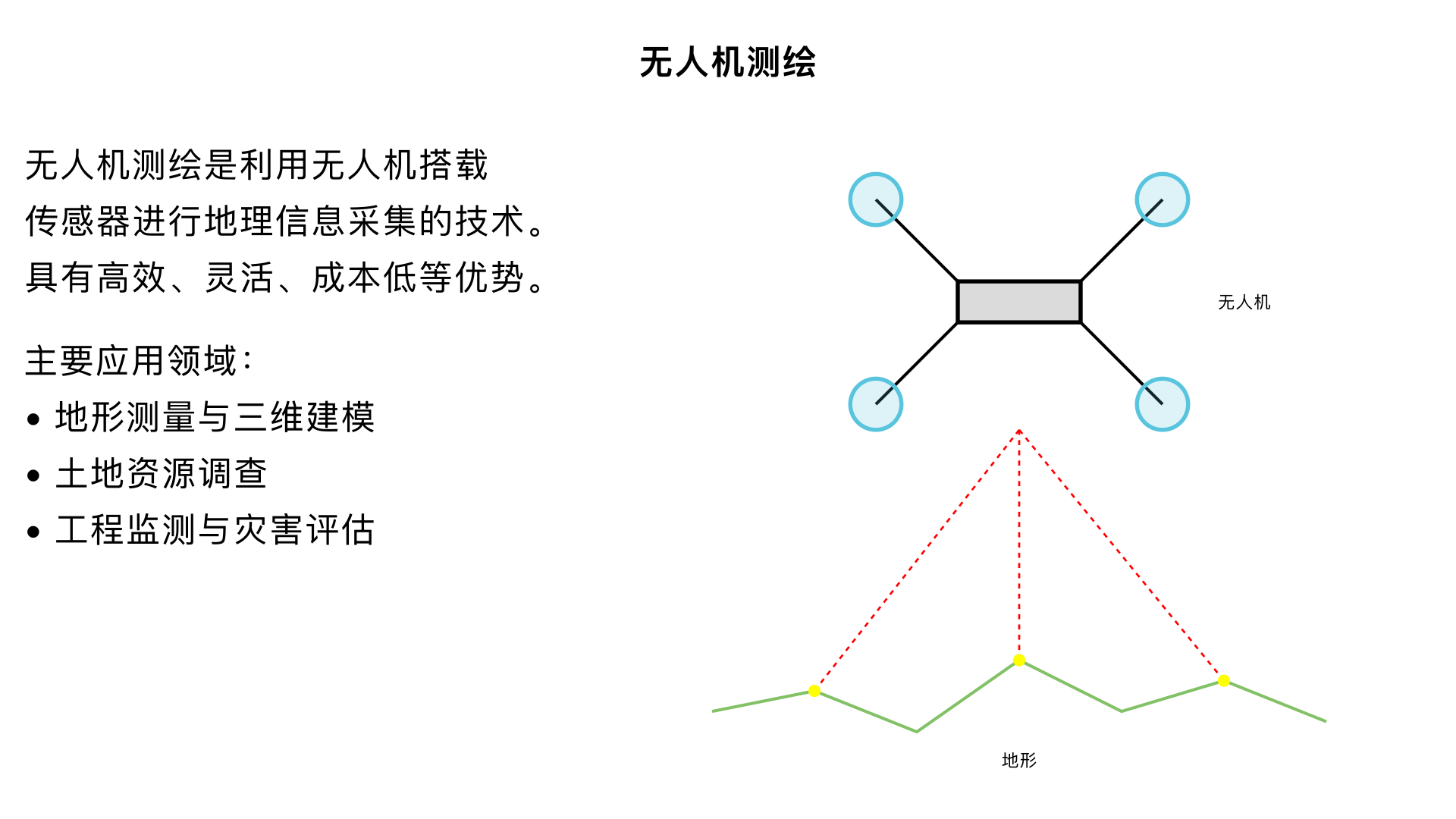
▶
无人机测绘
▶
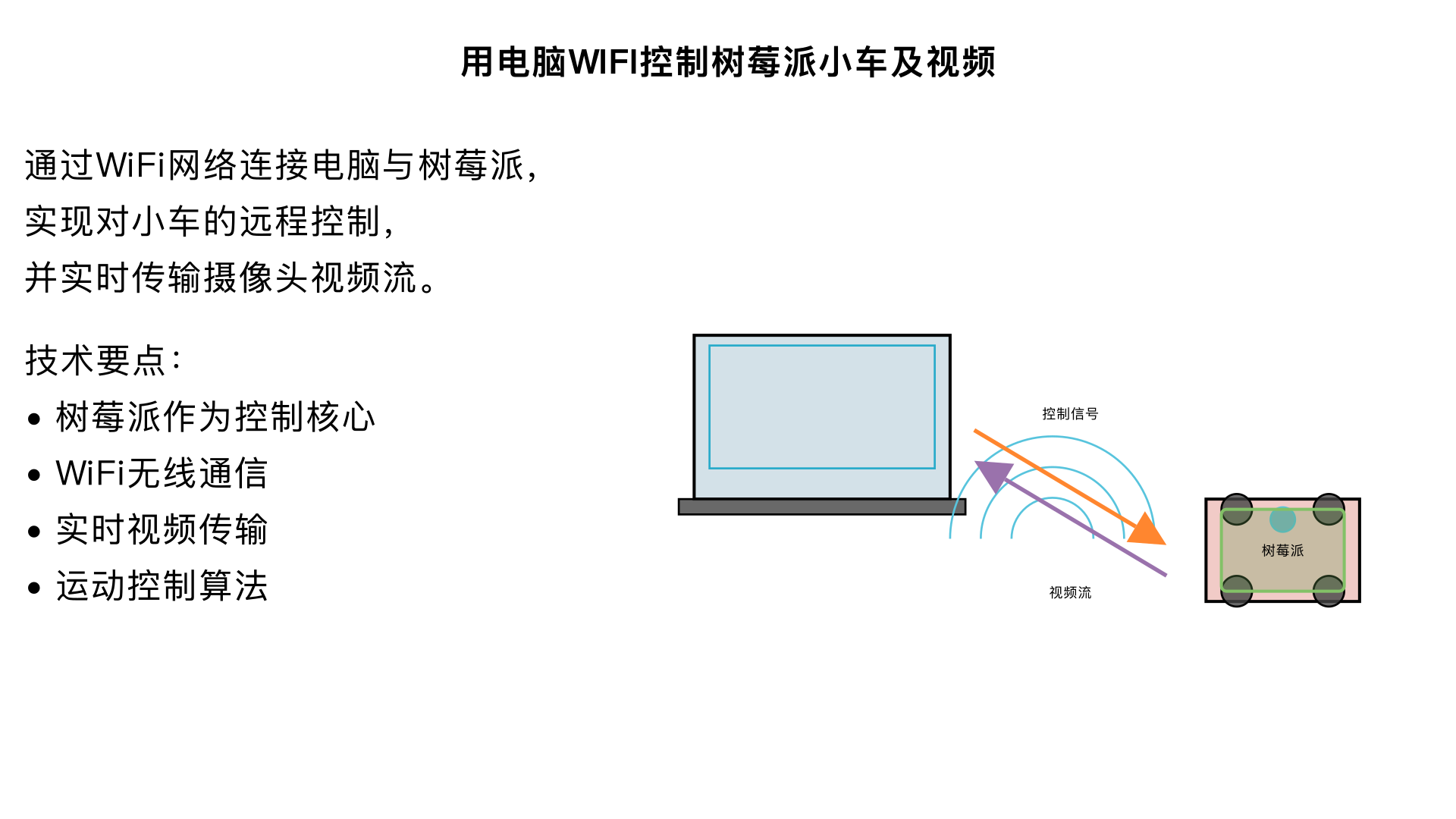
用电脑WIFI控制树莓派小车及视频
▶
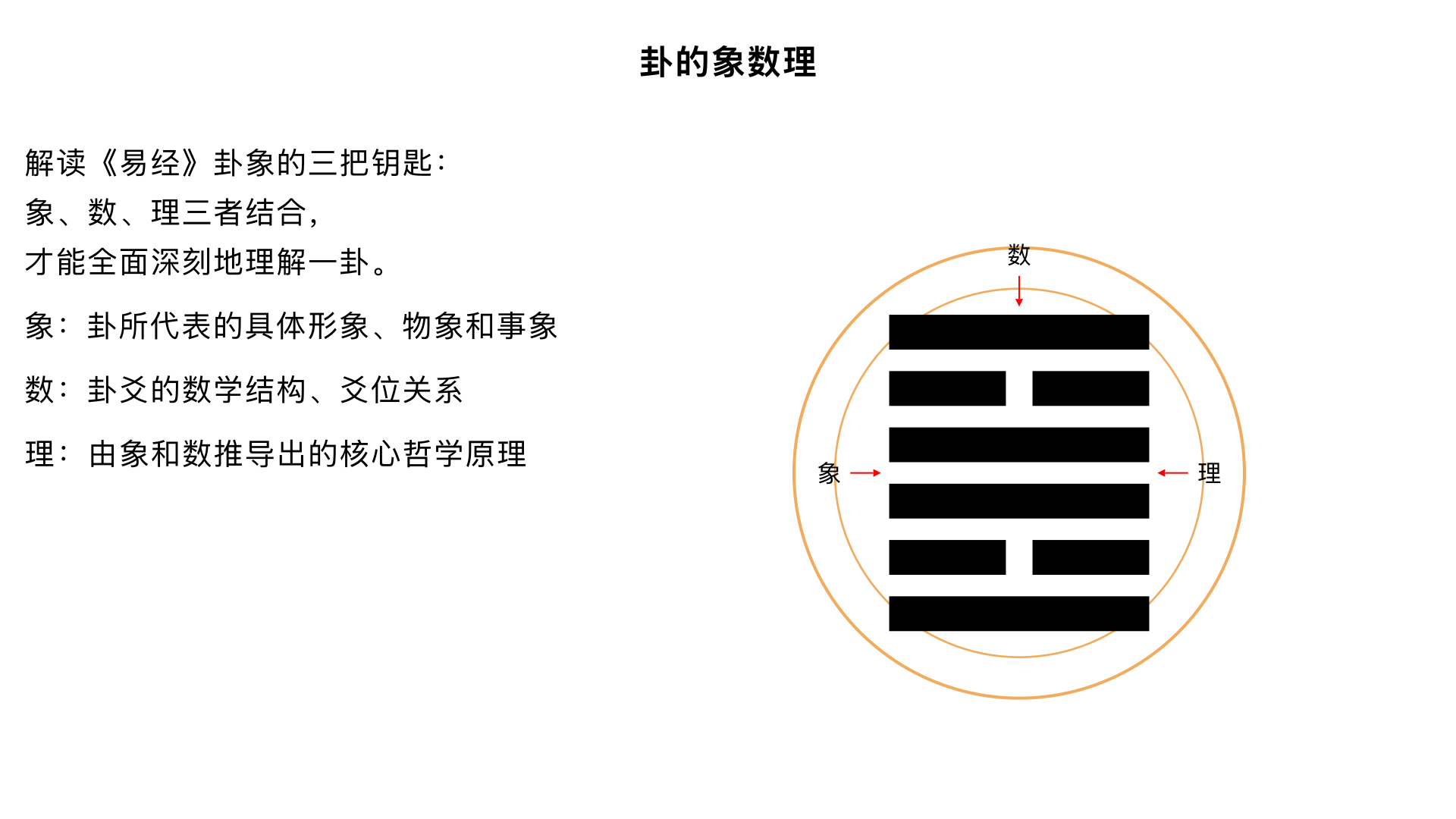
14、卦的象数理 核心内容:揭示解读任何一个卦所必须掌握的三个核心维度——象、数、理,这是打开《易经》大门的三把钥匙。 关键要点: 1. 象(现象/象征):卦所代表的具体形象、物象和事象(如乾为天、为君、为首)。 2. 数(规律/逻辑):卦爻的数学结构、爻位关系(承乘比应)和变化次序。 3. 理(道理/法则):由象和数推导出的核心哲学原理与人生启示。三者结合,才能全面、深刻地理解一卦。
▶
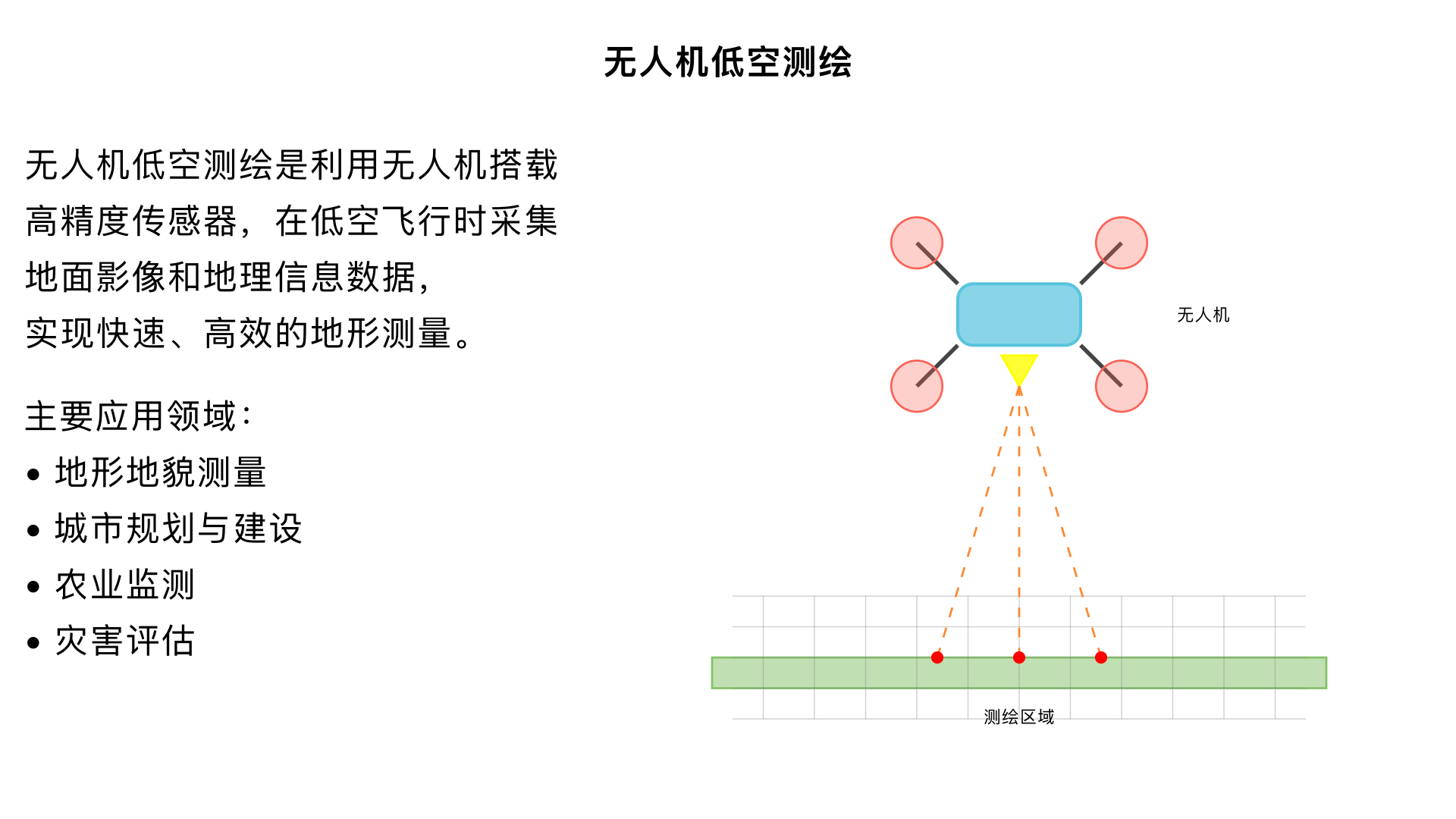
无人机低空测绘

▶
React
▶
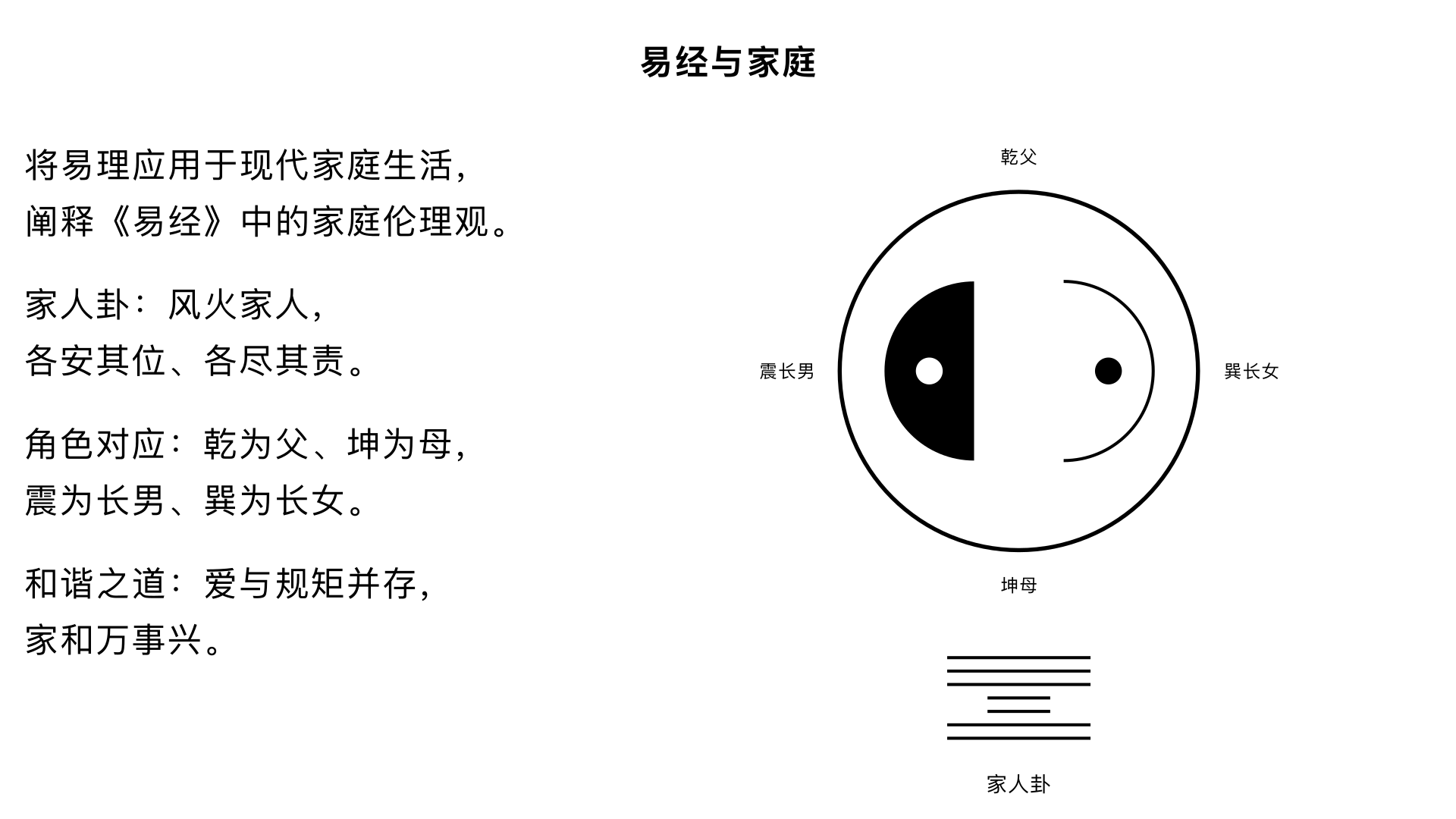
易经与家庭 核心内容:将易理应用于现代家庭生活,阐释《易经》中的家庭伦理观(如家人卦),探讨如何构建和谐稳固的家庭关系。 关键要点: 1. 家庭卦象:重点解析“风火家人”卦,强调各安其位、各尽其责、情感交流的家庭伦理。 2. 角色对应:八卦可类比家庭角色:乾为父、坤为母,震为长男等,阐明不同角色的责任与相处之道。 3. 和谐之道:家庭和谐的基础是爱与规矩并存,最终实现“家和万事兴”。
▶
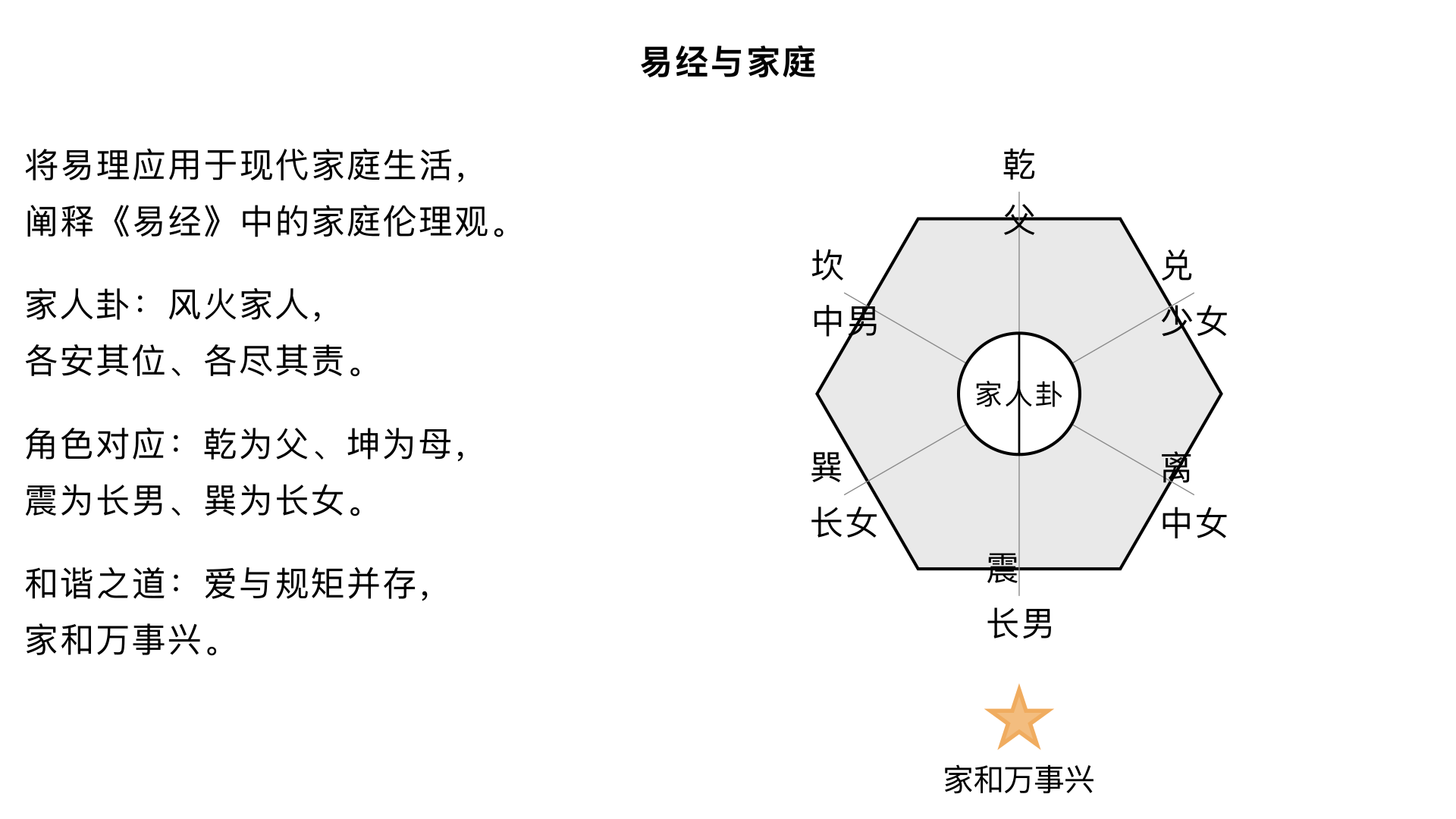
第13集、易经与家庭 核心内容:将易理应用于现代家庭生活,阐释《易经》中的家庭伦理观(如家人卦),探讨如何构建和谐稳固的家庭关系。 关键要点: 1. 家庭卦象:重点解析“风火家人”卦,强调各安其位、各尽其责、情感交流的家庭伦理。 2. 角色对应:八卦可类比家庭角色:乾为父、坤为母,震为长男等,阐明不同角色的责任与相处之道。 3. 和谐之道:家庭和谐的基础是爱与规矩并存,最终实现“家和万事兴”。
▶
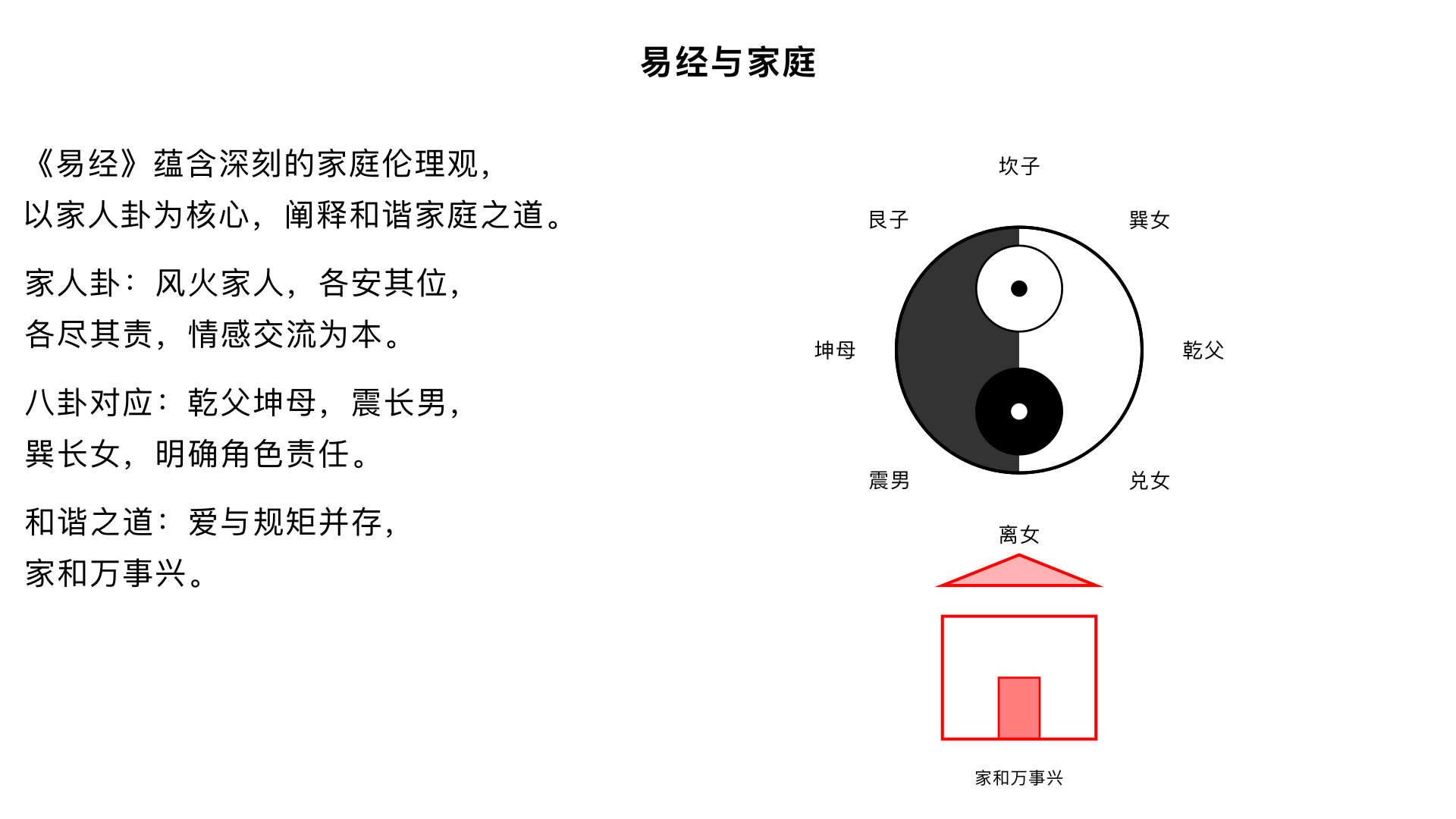
主题13、易经与家庭 核心内容:将易理应用于现代家庭生活,阐释《易经》中的家庭伦理观(如家人卦),探讨如何构建和谐稳固的家庭关系。 关键要点: 1. 家庭卦象:重点解析“风火家人”卦,强调各安其位、各尽其责、情感交流的家庭伦理。 2. 角色对应:八卦可类比家庭角色:乾为父、坤为母,震为长男等,阐明不同角色的责任与相处之道。 3. 和谐之道:家庭和谐的基础是爱与规矩并存,最终实现“家和万事兴”。
▶
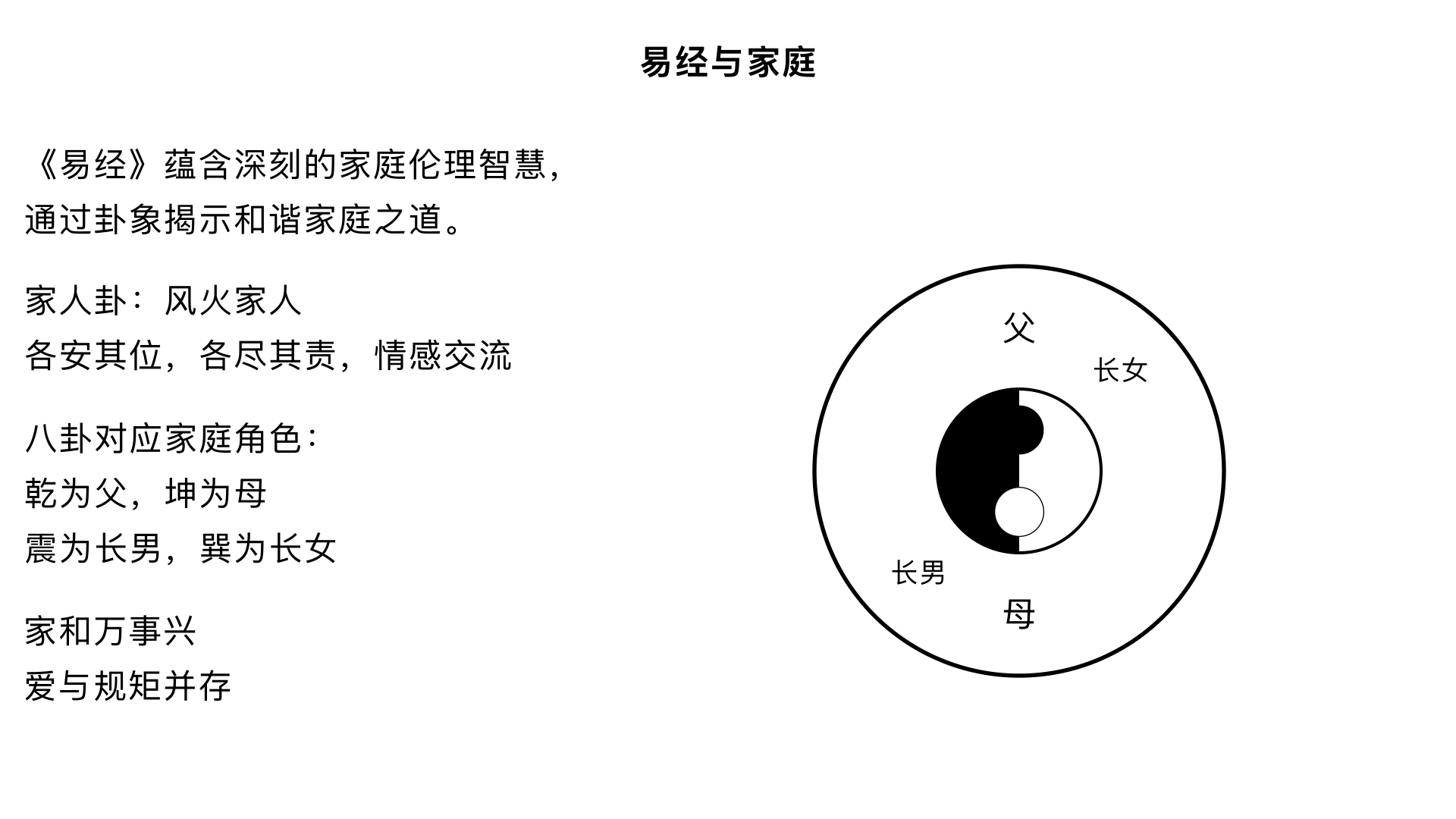
13、易经与家庭 核心内容:将易理应用于现代家庭生活,阐释《易经》中的家庭伦理观(如家人卦),探讨如何构建和谐稳固的家庭关系。1313、 关键要点: 1. 家庭卦象:重点解析“风火家人”卦,强调各安其位、各尽其责、情感交流的家庭伦理。 2. 角色对应:八卦可类比家庭角色:乾为父、坤为母,震为长男等,阐明不同角色的责任与相处之道。 3. 和谐之道:家庭和谐的基础是爱与规矩并存,最终实现“家和万事兴”。
▶
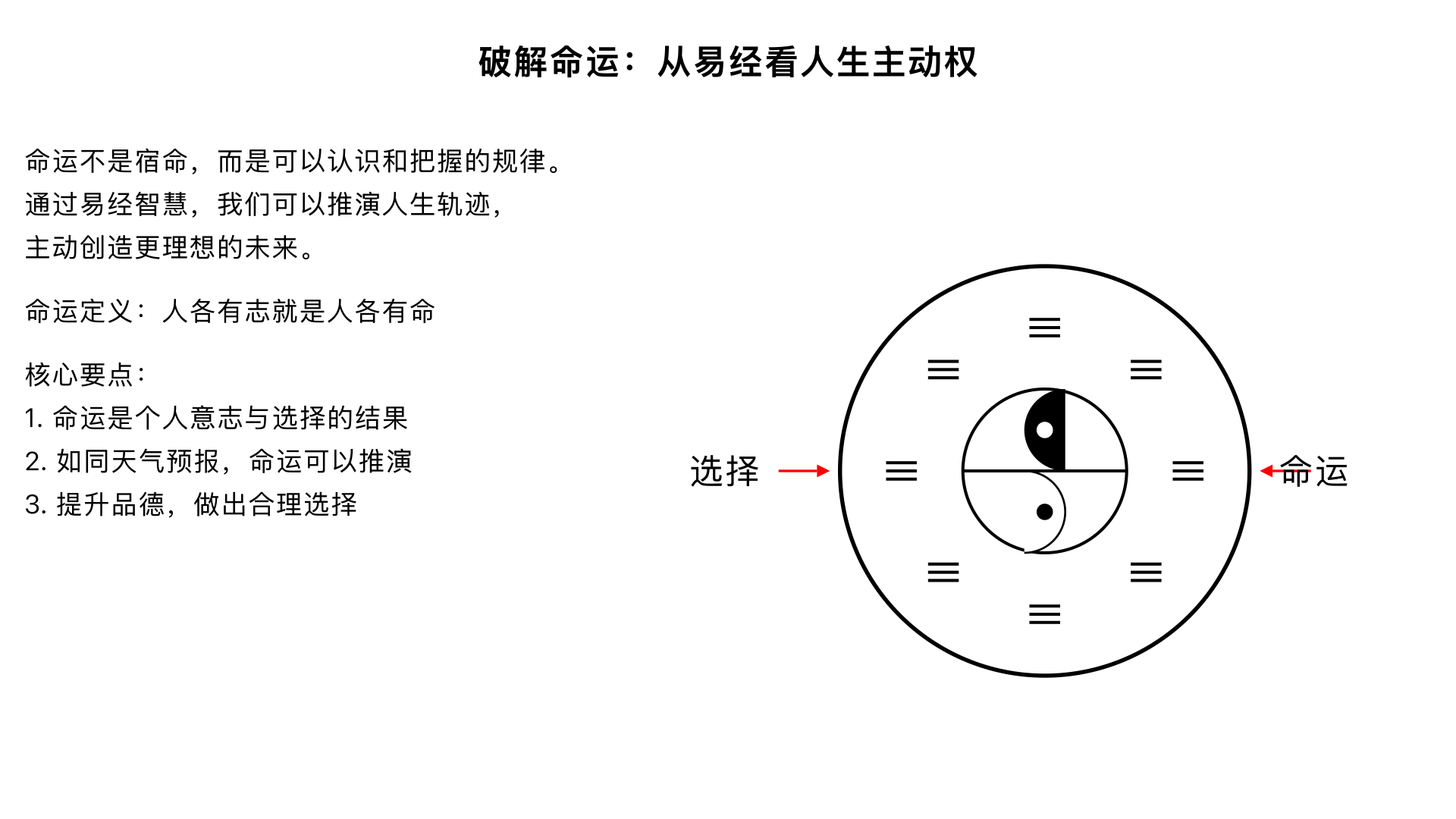
主题12、破解命运 核心内容:从《易经》角度探讨“命运”的本质,论证命运是一种可以认识和把握的“自然规律”,从而将人生的主动权交还给自己。 关键要点: 1. 命运定义:“人各有志就是人各有命”,命运是个人意志与选择长期作用下的结果,是一种潜在的规律。 2. 可知可改:如同天气预报,命运(人生轨迹)也可以通过《易经》智慧进行推演和把握。 3. 主动创造:核心在于了解规律、提升品德、做出合理选择,从而创造更理想的命运。
▶
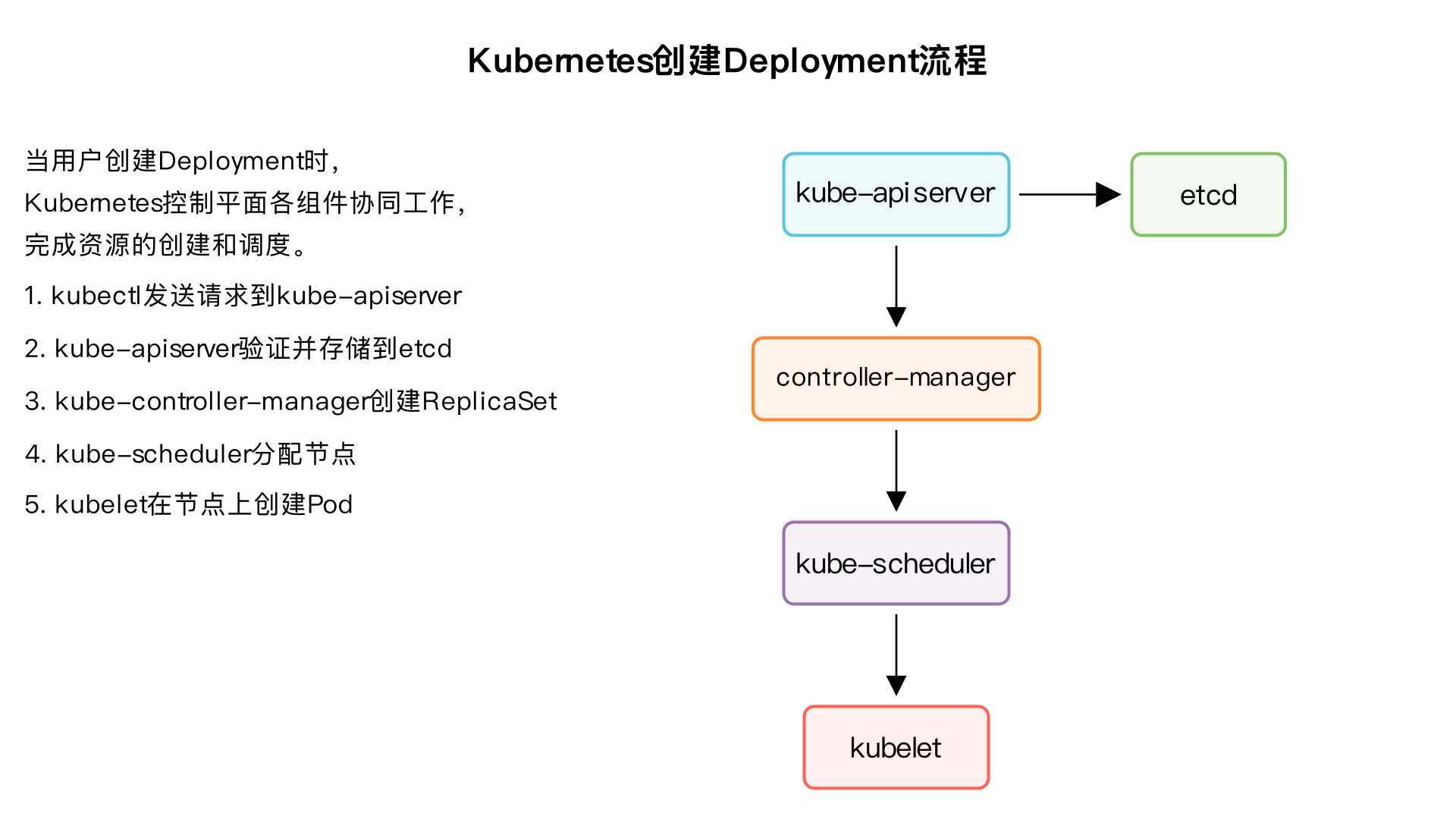
请帮我生成一段kubernetes创建deployment时,各控制平面组件的协作流程。要包含kube-apiserver,kube-suleduler,kube-controller-manager,kubelet,etcd,前后顺序一定要搞对
▶